强连通分量 Tarjan 算法

强连通

若一张有向图的节点两两互相可达，则称这张图是强连通的。

强连通分量(Strongly Connected Components，SCC)：

极大的强连通子图。

搜索树：

对图深搜时，每一个节点只访问一次，被访问过的节点与边构成搜索树。

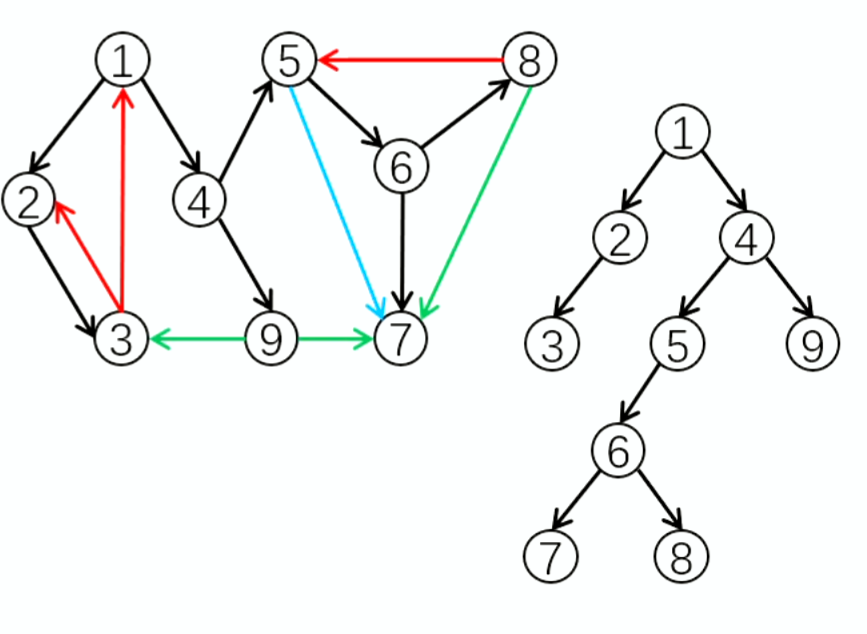
有向边按访问情况分 4类:

1. 树边(tree edge):访问节点走过的边。图中的黑色边。
2. 返祖边(back edge):指向祖先节点的边。图中的红色边。
3. 横叉边(cross edge):右子树指向左子树的边。图中的绿色边。
4. 前向边 (forward edge):指向子树中节点的边，图中的蓝色边。

边返祖边与树边必构成环，横又边可能与树边构成环。前向边无用

如果节点 $u$ 是某个强连通分量在搜索树中遇到的第一个节点，那么这个强连通分量的其余节点肯定是在搜索树中以 $u$ 为根的子树中。节点 $u$ 被称为这个强连通分量的根。

tarjan算法

变量

1. 时间戳 $dfn[u]$，节点 $u$ 第一次被访问的顺序
   
2. 追溯值 $low[u]$，从节点 $u$ 出发，能访问到的最小时间戳
   
3. 判断栈中元素 $instk[u]$，判断 节点$u$ 是否在栈中

操作

深搜到 $u$ 时，盖戳，入栈

枚举 $u$ 的邻边 $v$，分三种情况：

1. 若 $v$ 尚未访问，对 $v$ 进行深搜，回到 $x$ 时，用 $low[v]$，更新 $low[u]$，因为 $u$ 能到达 $v$，因此 $v$ 能到达的点 $u$ 也能到达
   
2. 若 $v$ 已经被访问过并且在栈中，说明 $v$ 是 $u$ 的祖先节点或者兄弟节点， 并且此时 $v$ 还在深搜过程中，因此用 $dfn[v]$ 更新 $low[u]$
3. r若 $v$ 已经被访问过并且不在在栈中，说明 $v$ 已经深搜完毕，其所在的强连通分量已经被处理，因此不用更新

更新完 $low[u]$ 后，若 $low[u]=dfn[u]$，则此时栈中到 $u$ 之前的元素都与 $u$ 在同一个强连通分量内，记录强连通分量所以点即可

例题

Luogu P2863 [USACO06JAN] The Cow Prom S

题目描述

有一个 $n$ 个点，$m$ 条边的有向图，请求出这个图点数大于 $1$ 的强连通分量个数。

输入格式

第一行为两个整数 $n$ 和 $m$。

第二行至 $m+1$ 行，每一行有两个整数 $\alpha$ 和 $b$，表示有一条从 $a$ 到 $b$ 的有向边。

输出格式

仅一行，表示点数大于 $1$ 的强连通分量个数。

数据范围

$2<n<{10}^4,2<m<5\times {10}^4,1<a,b<n$

code:

#include <bits/stdc++.h>

using namespace std;

const int N = 100010;

int n, m;
vector<int> h[N];
int dfn[N], low[N], tot;   
int stk[N], instk[N], top;
int sz[N], cnt;

void tarjan(int u)
{
    dfn[u] = low[u] = ++tot;
    stk[++top] = u;
    instk[u] = 1; 
    for (int i = 0; i < h[u].size(); i++)
    {
        int v = h[u][i];
        if (!dfn[v])
        {
            tarjan(v);
            low[u] = min(low[u], low[v]);
        }
        else if (instk[v]) low[u] = min(low[u], dfn[v]);
    }

    if (dfn[u] == low[u])
    {
        int v;
        cnt++;
        do
        {
            v = stk[top--];
            instk[v] = 0;
            sz[cnt]++;
        }while (u != v);
    }
}

int main()
{
    cin >> n >> m;
    for (int i = 0; i < m; i++)
    {
        int a, b;
        cin >> a >> b;
        h[a].push_back(b);
    }

    for (int i = 1; i <= n; i++)
        if (!dfn[i])
            tarjan(i);

    int res = 0;
    for (int i = 1; i <= cnt; i++)
        if (sz[i] > 1)
            res++;
            
    cout << res << endl;

    return 0;
}